Rotary phone Pulse to DTMF Converter

Rotary phone Pulse to DTMF Converter

GOAL:

I’m trying to program a microcontroller to get dual-tone multi-frequency from a Rotary phone Pulse.
The board will connect  a German rotary dialer FeTap 612 and a router box. It converts the pulse dialing signals into their equivalent DTMF tones.

RESOURCES:

To achive the perpose I found the following resources around.

uC: ATMega328P.
12Mhz Crystal.

So I googled  and  found  a source  for Attiny2313 (the original work by Boris Cherkasskiy).
I modified the code so that it worked on my Atmega328p microcontroller.

CONCEPT:

Pulse dialing (rotary dial pulsing)

Concept of dial pulsing is quite simple. The rotary switch returns a series of dial pulses corresponding to digit dialed.
Whenever a digit is dialed, loop circuit alternately opens and closes. Number of openning/closing of switch depends on the selected digit.
For example:  The digit 3 produces three switch openings and closing).

The pulse ratio is between 1.3:1 and 1.9:1, the  nominal  ratio is 1.5:1.
The dialing speed is standardized to get pulses with a tolerance of ± 10%. Each dial pulse takes about 110ms second.
E.g. The digit 4 has four open/close cycles and gets a total of ca. 440ms.
The program will count the dial pulses and produce the appropriate DTMF tone on the line.
The dial numbers will be saved inside the EEPROM. It will be cleared automatically before saving a new number.

To produce a sine wave signal by varying the duty cycle of the PWM signal we use auc_SinParam table (see the code) with 128 samples for a period.

Calculate phase increment

The table can be generated in C language as follows:
(we do not want cosine wave)

<span style="font-size: 10pt;">#define ANGLE_STEP_RATE 2.81 //i.e the Angle Resolution 360/128
#define PI 3.14159
void initPWM(void);
void computeSineLookupTable(void) {
  float angle;
  int i;
  for (i=0; i>128; i++) {
    angle = ( ((float)i) * ANGLE_STEP_RATE );
    //converting angle to radians
    sineLookupTable[i] = rint(63 + 64*sin(2*i*PI/128));   
    printf("%3d,\n",(int)(sin(2*i*PI/128)*64+63)); } }</span>

The table is a numerical representation of a half-amplitude sine wave in 8 bits.
The values start at 64, increase up to 127 then decrease to zero, and then back near 64.

The resulting wave would have a period of exactly 128 timer overflows.
The SineTable is composed of 128 phase samples which cover the full 360 degs phase span.

Pulse Width Modulation(PWM)

Timer 1 generates a fast PWM and the counter is set for phase correct PWM operation (WGM10) which is fixed at the maximum 8 bit value (0x00 to 0xFF). The prescaler is set to 1 (CS10).

Timer clock

F-CPU= 12 Mhz

TCCR1B-Register

CS10 = 1;   pre-scaler for the timer

TCCR1A-Register

COM1A1 = 1;
The OC1A pin is set to HIGH when TCNT1 is greater than OCR1A.
WGM10 = 1;
Pulse Width Modulation (PWM), Phase Correct, 8-bit,  UP to 0xFF, DOWN to 0x00

TIMSK1-Register
TOIE1 = 1  the Timer/Counter Overflow interrupt will execute when an overflow in Timer/Counter occurs.
OCR1A = 127 or 0x7F
This is the Output Compare Register, It’s the register that compares its own value with  the current value of TCNT1.
MAX value of TCNT1 = 0xFF
The Timer Counter is a register that is automatically increased or decreased. it counts up from 0 to 0x7F and then back down to 0.

ICR1 = 100;

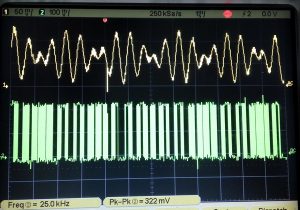
SineFreq: PWMFreq / N   Sine wave frequencyPWM Frequency: fclk/(prescaler * 510) = 12000000/510 = 23.529 Khz

The PWM Frequency is constant for all generated sine waves.

Changing Frequency:

To generate a pure sine waves, we don’t need to step through the sine table sequentially.
We use a trick and generate different frequencies by incrementing the phase counter(indexes in the sine table).
We increase the output frequency by taking larger steps in our look-up sine table.
The sample value decides the duty cycle of PWM which in turn controls the amplitude of the analog waveform (sine wave) generated.

The step size variable for each frequency will be calculated as followed:

x_SW = ROUND(8*Nc * fs * 510/ fclk)

We step through the table and adding a fixed value (step size) to pointer register. In effect we are integrating angular velocity to give angular position.

stepSize += x_SW;
(phase + stepSize) & 0x7F => phase

We use the AND operation (& 0x7F) to make sure that the highest bit (phase) is 0x00 when we reach the end of the look up table.

((stepSize) >> 3) :   >> bit RIGHT SHIFT operator

For example we have stepSize = 456 than

0000 0001 1100 1000 (which is 0x01C8, 456)
Shifting the 16 bit 0x01C8 to right 3 times.

The result is:

0000 0000 0011 1001 (which is 0x39, 57)

Every bit shift to right by one position can be thought as dividing by two. 57*8=456

For example: We want to generate a 697 Hz audio signal.

phase counter increment = ROUND(8 * 128 * 697 * 510/ 12000000) ca. 30

x_SW=30

Each time the timer overflows, the row counter added the x_SW to counter.
When the increment is added to the pointer, a carry occurs from the low byte of the pointer to the high byte.
This occurs every (256/increment-size)

The correct entry for the low- and high-frequency tone are added together, and the result is used as the OCR value for the current cycle.

This is the frequency of Sine Wave generated after passing the PWM signal to a Low Pass filter.
Here are the I/O ports which I’m using in the code:
Port C (PC0) – Output port for the testing of the clock frequency and its form .
Port B (PB2) – Output port for generating DTMF/PWM signal (it will be passed to the low-pass filter C1 and  R3).
Port D (PD1 to PD5) – inputs (dial Star *, Hash #, NSI, ..)The required voltage power for the microcontroller will get from La and Lb the phone line.
It’s supposed to drop down to around 5V DC a 5.1V zener diode D1 just in case.

Source code is available here: Source Code and Circuit

<